|
概说
依照候选数法概说一文中,候选数表的制作规则,我们可以知道:可以填入某一
个宫格的数字,一定会列于该宫格的候选数中;不在候选数中的数字,就不能填入该宫格中。
所以如果在候选数表中发现某一个宫格的候选数仅有 1 个数字,那就是表示:不必再考虑了!这个宫格就是
只能填入这个数字啦!如果填入别的数字,就会违反数独的填制规则的。
利用“找出候选数表中,候选数仅有 1 个数字的宫格来,并填入该候选数”的方法就叫做唯一候选数法(Singles Candidature,
sole Candidate)。
唯一候选数法示例
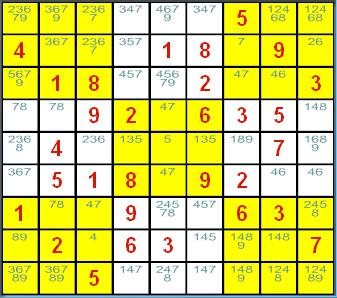
<图 1>数独谜题的候选数表
<图 1> 是我们在候选数法概说一文中完成的候选数表,其中有好几个宫格的候选数 都只有 1
个,所以可以利用唯一候选数法来进行填制。先还不要填入数字,我们先来找找看,有哪些宫格有 唯一候选数?
在 (2, 7) 有唯一候选数
7。
在 (5, 5) 有唯一候选数 5。
在 (8, 3) 有唯一候选数 4。
哇!同时出现了 3 个唯一候选数啊!那么,先填入哪一个会不会影响填制结果呢?当然不会了, 只要你高兴,喜欢先填哪一个都没问题的。
好,就在这 3 个宫格中填入他们的唯一候选数吧,填制结果如<图 2>:
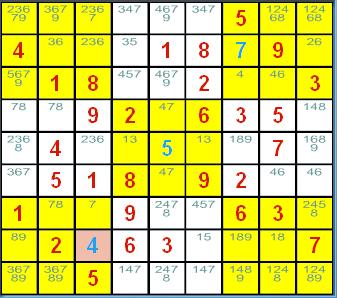
<图 2>
哇!又有唯一候选数出现了呢!没错,一般简易级的数独谜题,如果使用直观式的 唯一解法及摒除法来解题,即使是数独老手,也要花费相当的工夫才能完成;
但是如果采用唯一候选数法,从候选数表制作完成开始,唯一候选数将一个一个接连不断的出现,轻轻松松的 就可以完成解题啦!<图 3> 是
<图 1> 的完成解。
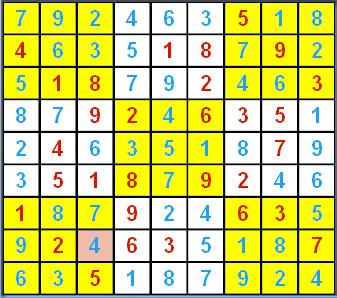
<图 3>完成解
|